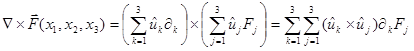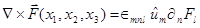9 OPERADOR DIFERENCIAL DE SEGUNDO ORDEN: LAPLACIANO

Operador de Laplace : El Operador de Laplace es un Operador Diferencial de segundo orden.  Se define, con base en el operador nabla, a manera de un producto punto de nabla consigo mismo:   

    

En notación usual :

En notación con índices :

En notación de suma :

O, más sencillamente:            

En notación compacta :

Utilizando el Operador de Laplace podemos definir dos operaciones que lo involucran:

Laplaciano de un campo escalar : Dado un campo escalar f(r), definimos El Laplaciano del campo escalar, como una Operación Diferencial Vectorial en la cual el Operador de Laplace, actuando sobre el campo escalar nos da como resultado un campo escalar.

En notación usual :

En notación con índices :

En notación de suma :

O, más sencillamente:            

En notación compacta :

El Laplaciano de un campo escalar se puede interpretar como la divergencia del gradiente del campo escalar:

Laplaciano de un campo vectorial : Dado un campo vectorial F(r), definimos El Laplaciano del campo vectorial, como una Operación Diferencial Vectorial en la cual el Operador de Laplace, actuando sobre el campo vectorial nos da como resultado un campo vectorial.

En notación usual :

En notación con índices :

En notación de suma :

O, más sencillamente:            

En notación compacta :

8 ROTACIONAL DE UN CAMPO VECTORIAL

Rotacional de un campo vectorial:  Dado un campo vectorial F(r), definimos el Rotacional del campo vectorial F(r), como una Operación Diferencial Vectorial en la cual el Operador Nabla, actuando a manera de producto cruz entre un vector y otro vector, nos da como resultado un campo vectorial :

En notación usual :

En notación con índices :

En notación de suma será: 

En notación compacta será:

Las propiedades del símbolo de Levi-Civita nos facilitarán ahora la expresión del Rotacional de un campo vectorial:

En notación de suma : 

En notación compacta :

Obsérvese que en esta expresión los índices m n i son tres índices mudos (hay tres sumas anidadas), lo cual corresponde a 3³ = 27 sumandos.

Puesto que

es un campo vectorial, podemos expresar alguna de sus componentes, así:

m-ésima componente de :

                   

Obsérvese que en esta expresión m es un índice flotante y n i dos índices mudos (hay dos sumas anidadas), lo cual corresponde a 3² = 9 sumandos.

Veamos como ejemplo:

primera componente de:

             
                       

Así mismo se tiene (verificarlo) :

7 DIVERGENCIA DE UN CAMPO VECTORIAL

Divergencia de un campo vectorial:  Dado un campo vectorial F(r), definimos La divergencia del campo vectorial, como una Operación Diferencial Vectorial en la cual el Operador Nabla, actuando, a manera de producto punto entre un vector y otro vector, nos da como resultado un campo escalar :

En notación usual : 

Con la convención   : 

En notación con índices :

Con la convención   :

En notación de suma : 

 Con la convención   : 

En notación compacta : 

 Con la convención   : 

6 GRADIENTE DE UN CAMPO ESCALAR

Gradiente de un campo escalar :  Dado un campo escalar f(r), definimos El Gradiente del campo escalar, como una Operación Diferencial Vectorial en la cual el Operador Nabla, actuando, a manera de producto ordinario entre un vector y un escalar, nos da como resultado un campo vectorial :

En notación usual :

Con la convención : 

En notación con índices :

Con la convención   :

En notación de suma :

  

Con la convención :

En notación compacta :

Con la convención :