Rotacional de un campo vectorial: Dado un campo vectorial F(r), definimos el Rotacional del campo vectorial F(r), como una Operación Diferencial Vectorial en la cual el Operador Nabla, actuando a manera de producto cruz entre un vector y otro vector, nos da como resultado un campo vectorial :
En notación usual :
En notación con índices :
En notación de suma será:
En notación compacta será:
Las propiedades del símbolo de Levi-Civita nos facilitarán ahora la expresión del Rotacional de un campo vectorial:
En notación de suma :
En notación compacta :
Obsérvese que en esta expresión los índices m n i son tres índices mudos (hay tres sumas anidadas), lo cual corresponde a 33 = 27 sumandos.
Puesto que
es un campo vectorial, podemos expresar alguna de sus componentes, así:
m-ésima componente de :
:
Obsérvese que en esta expresión m es un índice flotante y n i dos índices mudos (hay dos sumas anidadas), lo cual corresponde a 32 = 9 sumandos.
Veamos como ejemplo:
primera componente de:
:
Así mismo se tiene (verificarlo) :
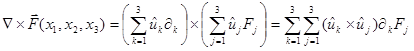
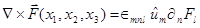
No hay comentarios:
Publicar un comentario