OPERACIONES CON VECTORES EN R3
PRODUCTO ORDINARIO DE UN VECTOR POR UN ESCALAR:
Dado un vector F ϵ R3 y un número real c ϵ R, el resultado del PRODUCTO ORDINARIO entre F y c es otro vector cuyas componentes rectangulares se obtienen de multiplicar las respectivas componentes de F por el número real c.
En notación usual será:
En notación con índices será:
En notación de suma será:
La j-ésima componente del vector Fc es: (Fc)j = Fjc
PRODUCTO PUNTO ENTRE DOS VECTORES:
Dados dos vectores F, G ϵ R, el resultado del PRODUCTO PUNTO entre F y G es un escalar el cual se obtienen de sumar los productos de las respectivas componentes de F y G.
Dados dos vectores F, G ϵ R, el resultado del PRODUCTO PUNTO entre F y G es un escalar el cual se obtienen de sumar los productos de las respectivas componentes de F y G.
En notación usual será:
En notación con índices será:
En notación de suma será:
=
En notación compacta será:
Delta de Kronecker: La delta de Kronecker es un símbolo matemático que en este desarrollo será de gran utilidad para el propósito de simplificar la notación. Se representa y define de la siguiente manera:
Es decir:
Orto-normalidad de la base canónica : Esto hace referencia a que los vectores de la base canónica son ortogonales (perpendiculares) entre sí y cada uno de ellos tiene norma uno. Lo anterior se puede expresar matemáticamente de la siguiente manera:
En notación usual :
En notación con índices :
En notación compacta :
Retomemos la expresión compacta del producto punto y utilicemos lo que acabamos de aprender:
En forma sencilla y fundamentalmente con carácter pedagógico se acostumbra decir que la delta de Kronecker aniquila una suma .
PRODUCTO CRUZ ENTRE DOS VECTORES: Dados dos vectores F, G ϵ R, el resultado del PRODUCTO CRUZ entre F y G es un vector el cual se obtienen de la siguiente manera:
En notación usual:
En notación con índices será:
En notación de suma será:
En notación compacta será:
Símbolo de Levi-Civita: El símbolo de Levi-Civita es un símbolo matemático que al igual que la delta de Kronecker será de gran utilidad para el propósito de simplificar la notación. Se representa y define de la siguiente manera:
con i,j,k = 1, 2,3
Una permutación impar corresponde al intercambio en la posición de dos índices consecutivos.
Una permutación par corresponde a dos permutaciones impares.
Así, por ejemplo:
y cualquier otro arreglo diferente de éstos es cero:
Es también importante entender las propiedades de permutación del épsilon:
Estas propiedades del símbolo de Levi-Civita nos facilitarán ahora la expresión vectorial del producto cruz:
En notación de suma :
En notación compacta :
Obsérvese que en esta expresión los índices m n i son tres índices mudos (hay tres sumas anidadas), lo cual corresponde a 33 = 27 sumandos.
Puesto que FXG es un vector, podemos expresar alguna de sus componentes, así:
m-ésima componente de FXG:
Veamos un ejemplo:
primera componente de FXG:
Así mismo se tiene (verificarlo) :
Contracción de Levi-Civita: La Contracción de Levi-Civita es un resultado muy interesante del Análisis Tensorial, el cual será una herramienta muy útil en la demostración de identidades vectoriales.
En notación de suma :
En notación compacta :
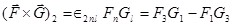
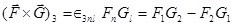
No hay comentarios:
Publicar un comentario